Notion de focale «idéale» en photographie

Définition simplifiée de la focale :

Le terme de focale «idéale» peut être compris comme la distance la plus juste par rapport à une surface de projection qui nous permette de restituer ce que voit l'oeil humain de façon normale (quoiqu'en vision monoculaire), sans distorsion.
En général, il s'agit de la diagonale du cadre d'image choisi.
Plus explicitement, il s'agit de la distance à partir de laquelle l'ensemble du cadre apparaît à notre regard avec une perspective qui paraît naturelle sans déformation perceptible entre les éléments proches et lointains.
On appelle aussi cette distance idéale : distance orthoscopique.

Figure 1 : Schéma de la coupe d'un appareil photographique.

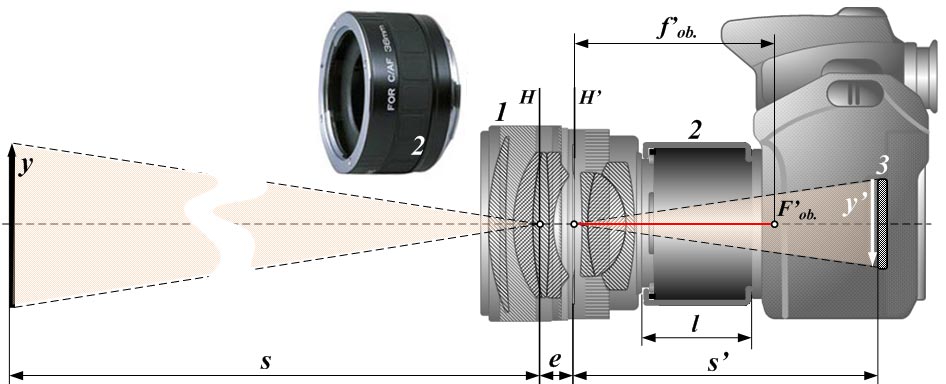
Dans 1 appareil photographique, on peut voir qu'il existe, en fonction des dimensions du sensor ou de la pellicule, une distance idéale pour laquelle ce qui est perçu par l'optique de l'appareil se retrouve reproduit exactement sur la pellicule.

La distance exprimée en millimètres détermine aussi la largeur du champ de vision (en degrés) appelé aussi en anglais, Field of View (FOV).

Figure 2 : Correspondances entre distances focales et champ de vision (FOV) calculés par rapport à la diagonale.

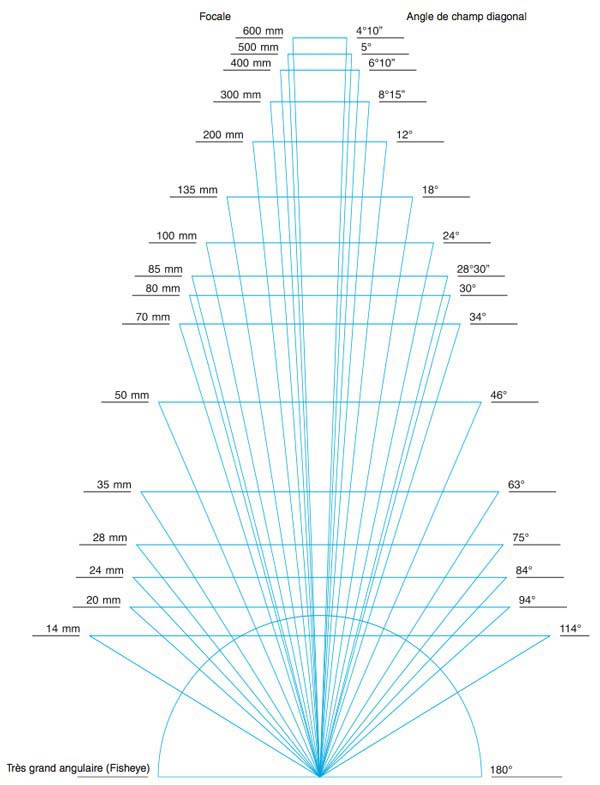
Si la distance focale augmente, alors le taux d'agrandissement augmente car le champ visuel diminue : on zoome sur une plus petite portion d'espace.
Dans le cas contraire, on élargie le champ de vision : les éléments vus par l'objectif sont rapetissés pour être ramenés au format de la pellicule.

L'idéal de la focale normale égale à la diagonale des formats standards donne :

• 6 x 6 : 79 mm (84.853)
• 4,5 x 6 : 70 mm (75)
• 6 x 7 : 91 mm (92.20)
• 24 x 36 : 43 mm (43.266)

Pour des raisons économiques et de standardisation des objectifs photographiques, les constructeurs d'optiques ont simplifié ou arrondi ces valeurs :

• 6 x 6 : 80 mm
• 4,5 x 6 : 80 mm
• 6 x 7 : 100 mm
• 24 x 36 : 50 mm

Empiriquement, les photographes professionnels choisissaient leur objectifs en vue d'une distance orthoscopique idéale, selon les règles suivantes :

• Standard : diagonale du format
• Petit télé-objectif : entre 2 × la longueur du format et 3 x la largeur du format
• Télé-objectif : entre 2 x la diagonale et 3 x la longueur du format
• Grand angle : la longueur du format
• Très grand angle : la largeur du format

Projection perspective et focale en Image de Synthèse

En image de synthèse, nous avons modifié ce schéma (cf Fig.1) pour traduire cette opération d'agrandissement ou de réduction avec un simple théorème : Thalès.

Ce schéma utilisé par tous les logiciels qui projettent une scène 3D en perspective s'appelle :

Il établi une relation d'homothétie interne entre l'objet dans le monde réel et sa projection en perspective sur l'image.

Figure 3 : Schéma de la Posture du Photographe.

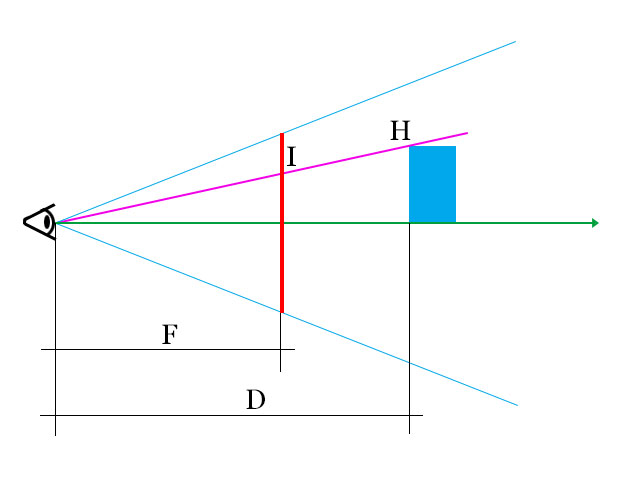
Règle d'homothétie interne basée sur le théorème de Thalès : I = H/D x F avec :

• H position d'un point dans l'espace dont on veut calculer la projection sur le support image.
• D distance entre le photographe et ce point.
• F distance focale entre le photographe et le support image.
• I Projection de H sur le plan de l'image.

Pour obtenir la conversion en focale de type photographique, chaque logiciel peut choisir 1 format photographique de référence distinct.
Ainsi si ces calculs se font par rapport à la diagonale, la largeur ou la hauteur de ce format, on obtient :


La dimension du support s'appelle couramment : APERTURE ou en français, OUVERTURE même si cela peut être confondu avec une autre notion (l'exposition).

Le 3^ème point de fuite

L'existence ou non d'un 3^ème point de fuite dans une image en perspective dépend moins de la position que de l'orientation de l'appareil photographique par rapport au sujet.
En général les photographes spécialisés dans la prise de vue d'oeuvres architecturales, préfèrent faire en sorte de supprimer ce 3^ème point de fuite : l'objectif est d'éviter que les déformations qui en résulteraient fassent perdre au spectateur le rapport entre les différentes dimensions du bâtiment.
Cependant, on perd alors la sensation de monumentalité, le rapport à l'échelle humaine.

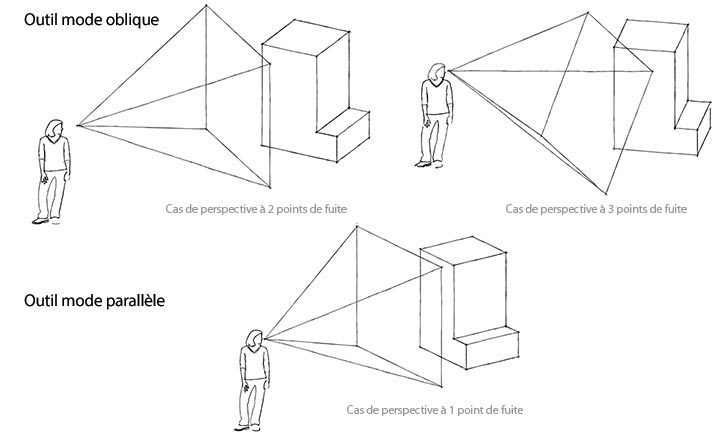
En pratique (cf Fig.4), si le plan du capteur photographique est parallèle aux lignes verticales du bâtiment photographié, il n'y a que 1 ou 2 points de fuite. Dans le cas contraire, il existe 1 point de fuite supplémentaire placé verticalement en haut ou en bas.
On a pris l'habitude de l'appeler : le 3^ème point de fuite.

(...) Il y a un point de fuite supplémentaire dès que les plans verticaux du bâtiment photographiés ne sont plus parallèles ou perpendiculaires au plan du capteur photographique (pellicule ou sensor).

Pour mieux comprendre quand ce point de fuite supplémentaire apparaît :
Si le point de visée de la prise de vue se situe plus haut ou plus bas que la position du photographe, alors la ligne d'horizon descend ou monte sur la photographie alors ce point de fuite apparaît.

• On appelle vue en plongée lorsque la ligne d'horizon remonte par rapport à l'axe horizontal central de la photographie (ou de l'image calculée).
• On parle de prise de vue en contre-plongée lorsque la ligne d'horizon redescend par rapport à l'axe horizontal central de l'image.

Figure 4 : L'orientation des plans de l'objet par rapport au plan de l'image de l'appareil détermine l'existence des différents points de fuite.

Galerie d'images de référence pour le cours à utiliser avec i3dexpress.
Enregistrer l'image de votre choix sur votre ordinateur pour l'ouvrir ensuite dans i3dexpress.fr à partir de l'onglet «FICHIERS».
Attention : ces images ne sont pas libres de droits et ne peuvent être utilisées qu'à titre d'exemple et en aucun cas pour une exploitation commerciale. Haut ▲